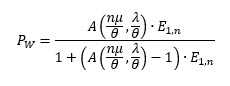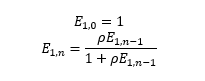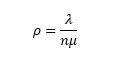Resumen de la fórmula de Erlang
El cálculo del número de recursos necesarios para cada día e intervalo se basa en el modelo Erlang A. El modelo Erlang A es una extensión del modelo Erlang C, por lo tanto, es necesario comprender Erlang C para entender Erlang A.
Erlang C
Erlang C es una fórmula de modelado de tráfico utilizada en centros de llamadas para determinar el número de recursos necesarios para mantener los tiempos de espera dentro de los objetivos del nivel de servicio del centro de contacto. Este método asume que todos los que llaman permanecen en la cola hasta que la llamada sea atendida, y por lo tanto puede sobreestimar el personal requerido. Al programar a los agentes, Erlang C también se puede usar para calcular el nivel de servicio previsto.
Erlang C basa su fórmula en tres factores: el número de agentes que brindan el servicio, el número de personas que llaman y esperan, y el tiempo promedio que toma atender a cada persona que llama.
Erlang A
La diferencia entre Erlang A y Erlang C es que Erlang A toma en cuenta la paciencia promedio, mientras que Erlang C asume que las personas que llaman tienen paciencia infinita. Si se establece la tasa de abandono para una habilidad en 0 %, esto equivale a usar Erlang C, ya que se está diciendo que nadie abandonará la cola.
La paciencia promedio es el tiempo promedio que una persona que llama está dispuesta a esperar antes de abandonar la cola. WFM utiliza la tasa de abandono para la habilidad para estimar la paciencia promedio. La paciencia promedio se utiliza para calcular la probabilidad de espera en la siguiente fórmula.
Cálculo de agentes necesarios
El cálculo del número de agentes necesarios con Erlang A utiliza estas medidas:
- Nivel de servicio
- Tiempo de servicio
- Número de llamadas
- Tiempo promedio de manejo
- Ocupación mínima
- Ocupación máxima
- Paciencia promedio con tasa de abandono
Cálculo del nivel de servicio previsto
El cálculo del nivel de servicio previsto con Erlang A utiliza estas medidas:
- Agentes programados
- Número de llamadas
- Tiempo promedio de manejo
- Tiempo de servicio
- Ocupación mínima
- Ocupación máxima
- Paciencia promedio con tasa de abandono
Fórmula
Esta fórmula se utiliza para calcular la probabilidad de que un cliente tenga que esperar para recibir servicio.
- Pw — Probabilidad de que un cliente tenga que esperar para recibir servicio.
- λ — Número de llamadas.
- µ — Tasa de servicio (1/µ = Tiempo promedio de manejo)
- n — Número de agentes.
- θ — Tasa individual de abandono (1/θ = Paciencia promedio).